双摆运动的数值解法
Published:
摘要
本文详细推导了双摆系统的运动方程,并通过数值方法进行求解.双摆系统由两个连接在一起的摆球组成,其运动由两个广义坐标 $\theta_1,\theta_2$ 描述.通过计算小球的动能和势能,得到了系统的拉格朗日函数,进而推导出拉格朗日方程.将拉格朗日方程化简并转化为矩阵形式,我们得到了描述双摆系统运动的矩阵方程 $A\Theta=b$ .利用Python编程语言及其科学计算库(如numpy,scipy和matplotlib),本文实现了双摆系统运动的数值求解和动画展示.数值求解采用solve_ivp方法求解微分方程组,初始条件包括时间范围,初始角度和初始角速度.最后,通过动画展示了双摆系统的动态行为.
引言
双摆系统是一个经典的力学模型,由两个串联的摆组成.它有着复杂的物理内涵,包括非线性动力学和混沌现象.与简单摆相比,双摆的运动方程更为复杂,它不仅依赖于摆长,摆质量和重力加速度,还受到各摆之间相互作用力的影响.这些特性使双摆成为研究非线性系统的理想实验平台. 双摆系统的独特之处在于它能够在一定条件下表现出混沌运动,这种运动极其敏感,对初始条件的微小变化都会导致截然不同的运动轨迹.因此,双摆的分析和模拟在物理学,工程学和复杂系统的研究中具有重要意义. 在本研究中,我们首先推导出双摆系统的运动方程,这些方程可以描述双摆在任意时刻的运动.接下来,我们将采用数值模拟方法对这些方程进行求解,分析双摆在不同初始条件下的特性.
双摆的运动方程推导
下面开始推导双摆的运动方程:
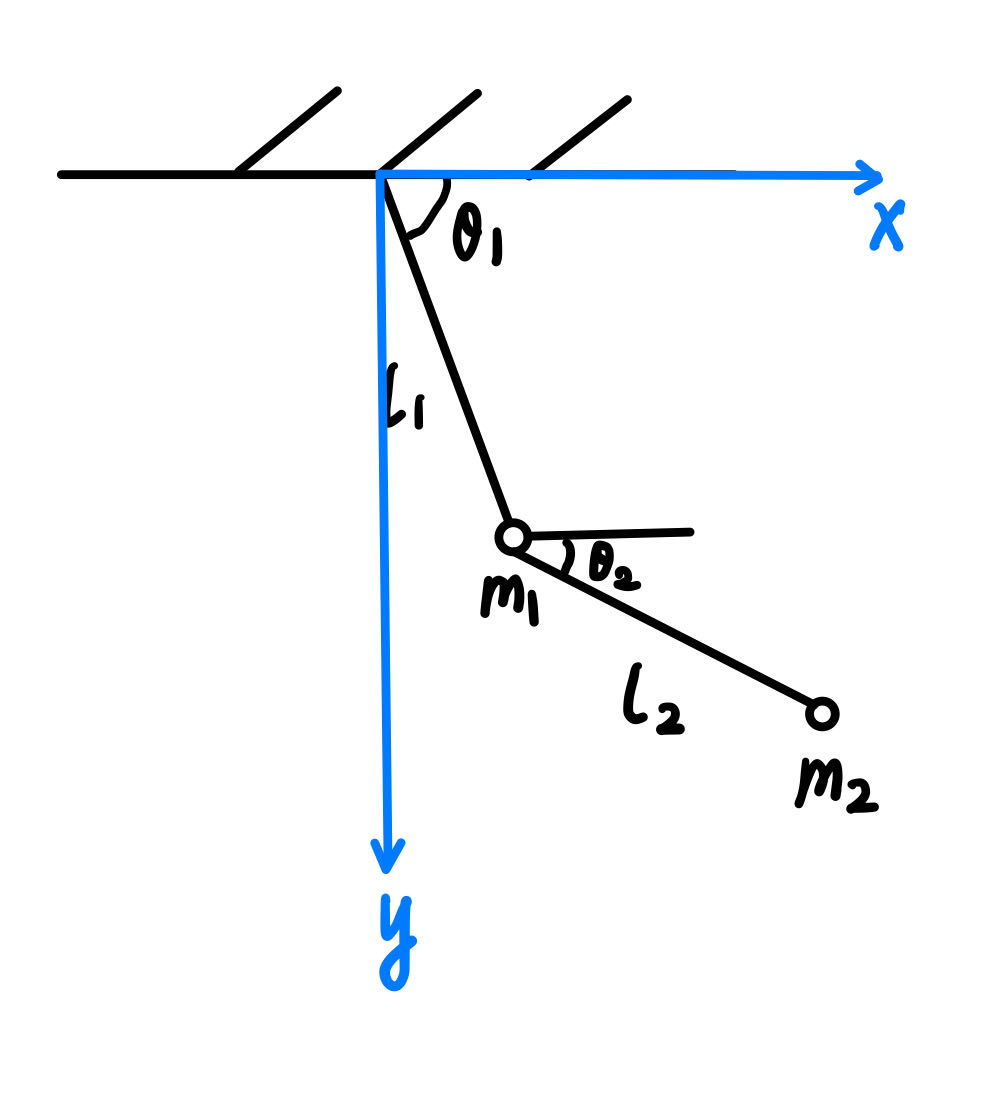
设广义坐标为 $\theta_1$ 和 $\theta_2$ ,则小球1的x,y坐标为:
\(x_1=l_1\cos{\theta_1} \quad y_1=l_1\sin{\theta_1}\)
小球2的x,y坐标为:
\[x_2 = l_1\cos{\theta_1}+l_2\cos{\theta_2}\quad x_2 = l_1\sin{\theta_1}+l_2\sin{\theta_2}\]将小球1,2的x,y坐标对时间求导数,得到
\[v_{x1}=-l_1\sin{\theta_1}\dot{\theta_1}\quad v_{y1}=l_1\cos{\theta_1}\dot{\theta_1}\] \[v_{x2}=-l_1\sin{\theta_1}\dot{\theta_1}-l_2\sin{\theta_2}\dot{\theta_2}\quad v_{y2}=l_1\cos{\theta_1}\dot{\theta_1}+l_2\cos{\theta_2}\dot{\theta_2}\]小球1的动能
\[T_1=\frac{m_1(v_{x1}^2+v_{y1}^2)}{2}=\frac{m_1l_1^2\dot{\theta_1}^2}{2}\]小球2的动能
\[T_2=\frac{m_2(v_{x2}^2+v_{y2}^2)}{2}=\frac{m_2[l_1^2\dot{\theta_1}^2+l_2^2\dot{\theta_2}^2+2l_1l_2\dot{\theta_1}\dot{\theta_2}\cos(\theta_1-\theta_2)]}{2}\]以天花板为零势能面,则小球1,2的势能
\[V_1=-m_1gl_1\sin{\theta_1}\quad V_2=-m_2g(l_1\sin{\theta_1}+l_2\sin{\theta_2})\]小球1,2系统的拉格朗日函数
\[L=T-V=T_1+T_2-V_1-V_2\]代入得
\(L=\frac{m_1l_1^2\dot{\theta_1}^2}{2}+\frac{m_2[l_1^2\dot{\theta_1}^2+l_2^2\dot{\theta_2}^2+2l_1l_2\dot{\theta_1}\dot{\theta_2}\cos(\theta_1-\theta_2)]}{2}+m_1gl_1\sin{\theta_1}+m_2g(l_1\sin{\theta_1}+l_2\sin{\theta_2})\)
对于广义坐标 $\theta_1$ ,有拉格朗日方程
\[\frac{d}{dt}(\frac{\partial L}{\partial\dot{\theta_1}})-\frac{\partial L}{\partial \theta_1}=0\]代入得
\(m_1l_1^2\ddot{\theta_1}+m_2l_1^2\ddot{\theta_1}+m_2l_1l_2\ddot{\theta_2}\cos(\theta_1-\theta_2)+m_2l_1l_2\dot{\theta_2}^2\sin(\theta_1-\theta_2)-(m_1+m_2)gl_1\cos\theta_1=0\)
对于广义坐标 $\theta_2$ ,有拉格朗日方程
\[\frac{d}{dt}(\frac{\partial L}{\partial\dot{\theta_2}})-\frac{\partial L}{\partial \theta_2}=0\]代入得
\(m_2l_2^2\ddot{\theta_2}+m_2l_1l_2\ddot{\theta_1}\cos(\theta_1-\theta_2)-m_2l_1l_2\dot{\theta_1}^2\sin(\theta_1-\theta_2) -m_2gl_2\cos\theta_2=0\)
化简两式得方程组
\[\begin{cases} (m_1+m_2)l_1\ddot{\theta_1}+m_2l_2\ddot{\theta_2}\cos(\theta_1-\theta_2)+m_2l_2\dot{\theta_2}^2\sin(\theta_1-\theta_2)-(m_1+m_2)g\cos\theta_1=0 \\ l_2\ddot{\theta_2}+l_1\ddot{\theta_1}\cos(\theta_1-\theta_2)-l_1\dot{\theta_1}^2\sin(\theta_1-\theta_2)-g\cos\theta_2=0 \end{cases}\]将方程组化简成矩阵形式,如果设
\[A=\begin{pmatrix} (m_1+m_2)l_1 & m_2l_2\cos(\theta_1-\theta_2) \\ l_1\cos(\theta_1-\theta_2) & l_2 \end{pmatrix}\] \[\Theta=\begin{pmatrix} \ddot{\theta_1} \\ \ddot{\theta_2} \end{pmatrix}\] \[b=\begin{pmatrix} (m_1+m_2)g\cos\theta_1-m_2l_2\sin(\theta_1-\theta_2)\dot{\theta_2}^2 \\ l_1\sin(\theta_1-\theta_2)\dot{\theta_1}^2+g\cos{\theta_2} \end{pmatrix}\]则有
\[A\Theta=b\]以上是双摆运动方程的推演.
双摆运动数值模拟的代码实现
接下来我们将展示代码的编写过程.
首先,让我们写出程序的思路:
1.导入库:导入所需的Python库(numpy, matplotlib, scipy等).
2.定义常量:定义物理常量、质量、长度和重力加速度.
3.定义微分方程函数df:通过解矩阵方程 $A\Theta=b$ ,返回两个广义坐标的一阶和二阶导数.
4.使用solve ivp求解微分方程组,其中时间范围,初始角度及角速度,步长设置和求解方法均可调节.
5.提取解的结果:从求解结果中提取时间、角度和角速度.
6.计算系统的坐标:将角度转换为实际坐标x,y,用于绘图.
7.设置绘图:初始化绘图区域和图形.
8.定义动画初始化函数init:设置动画的初始状态.
9.定义动画更新函数update:定义每一帧的更新内容.
10.创建动画并保存:使用FuncAnimation创建动画,并将其保存为视频文件.
11.展示动画
以下是程序代码
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from scipy.integrate import solve_ivp # 导入所需的Python库
m1=1
m2=1
l1=1
l2=1
g=9.8 #定义所需数值
def df(t,variables): #定义微分方程函数df
th1,th2,om1,om2=variables #th1,th2为角度,om1,om2位角速度
A=np.zeros((2,2))
b=np.zeros(2) #定义矩阵
#给矩阵元素赋值
A[0,0]=l1*(m1+m2)
A[0,1]=m2*l2*np.cos(th1-th2)
A[1,0]=l1*np.cos(th1-th2)
A[1,1]=l2
b[0]=(m1+m2)*g*np.cos(th1)-m2*l2*np.sin(th1-th2)*om2**2
b[1]=l1*np.sin(th1-th2)*om1**2+g*np.cos(th2)
dom1,dom2=np.linalg.solve(A,b) #解矩阵方程得到角加速度
return np.array([om1,om2,dom1,dom2])
sol=solve_ivp(df, [0,10],[0,-np.pi/6,0,0],t_eval=np.linspace(0,10,500),method='RK45') #用solve_ivp求解微分方程组,时间范围为0-10秒,初始角度为0,-pi/6,初始角速度为0
t=sol.t
th1=sol.y[0]
th2=sol.y[1]
om1=sol.y[2]
om2=sol.y[3] #提取出角度,角速度
x1=l1*np.cos(th1)
y1=-l1*np.sin(th1)
x2=x1+l2*np.cos(th2)
y2=y1-l2*np.sin(th2) #化成直角坐标
#设置绘图
fig=plt.figure(dpi=144)
ax=fig.gca()
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
ax.set_aspect("equal")
ax.grid()
pendulum,=ax.plot([],[],"-o",lw=2)
time_mark=ax.text(0.05,0.9, '',transform=ax.transAxes)
#定义动画初始化函数init
def init():
x=[0.0,x1[0],x2[0]]
y=[0.0,y1[0],y2[0]]
pendulum.set_data(x,y)
time_mark.set_text('')
return pendulum,time_mark
#定义动画更新函数update
def update(num):
x=[0.0,x1[num],x2[num]]
y=[0.0,y1[num],y2[num]]
pendulum.set_data(x,y)
time_mark.set_text('time = %.1fs'%(num*0.02))
return pendulum,time_mark
#使用FuncAnimation创建动画,并将其保存为视频文件
ani=FuncAnimation(fig,update,frames=range(len(y1))
,interval=20,blit=True,init_func=init)
ani.save('双摆.mp4',writer='ffmpeg')
#展示动画
plt.show()
动画展示
结论与展望
结论
本文通过数值方法求解了双摆运动的方程,详细推导了广义坐标 $\theta_1,\theta_2$ 对应的小球在不同位置的动能和势能,并结合拉格朗日方程得出了双摆系统的运动方程.我们利用Python代码,使用solve_ivp函数求解了微分方程组,并通过动画展示了双摆的运动过程.研究表明,双摆系统的运动具有高度的非线性和复杂性,即使在初始条件相近的情况下,系统也会展现出完全不同的运动轨迹.这进一步验证了双摆运动的混沌特性.
展望
未来的研究可以在以下几个方面进行扩展和深入:多摆系统的研究:本文仅讨论了双摆系统,未来可以将研究对象扩展到多摆系统,探讨更多摆体之间的相互作用及其对系统运动的影响.初始条件的敏感性分析:可以进一步研究双摆系统对初始条件的敏感性,量化混沌行为的程度,并通过李雅普诺夫指数等方法进行分析.阻尼和外力的影响:考虑引入阻尼和外力对双摆运动的影响,研究实际物理系统中能量耗散和外界驱动力对系统运动的影响.优化数值算法:在数值求解方法上,可以尝试更多高效,精确的数值算法,提高计算的稳定性和精度,以适应更复杂的系统和更长时间的模拟.实验验证:通过实际物理实验验证数值模拟结果,进一步确认模型的准确性和适用性,促进理论与实践的结合.通过上述研究,我们能够进一步加深对非线性动力学系统的理解,为相关领域的研究提供更有力的理论支持和实践指导.